Hàm số mũ và logarit là chuyên đề quan trọng trong chương trình toán học lớp 12. Vậy logarit là gì? Bảng công thức logarit và đạo hàm như nào? Kiến thức về công thức đổi cơ số logarit? Bí quyết ôn thi và cách nhớ công thức về logarit? Trong bài viết dưới đây, Gockhampha.edu.vn.Com.Vn sẽ giúp bạn tổng hợp bảng công thức logarit cùng những nội dung liên quan.
Bạn đang đọc: Logarit là gì? Tổng hợp công thức logarit đầy đủ, chính xác | Toán 12
Contents
Định nghĩa logarit là gì?
- Logarit theo định nghĩa chính là phép toán nghịch đảo của lũy thừa. Do đó, logarit của một số là số mũ của một giá trị cố định, gọi là cơ số, và phải được nâng lên lũy thừa để tạo ra con số đó. Logarit cũng được hiểu là đếm số lần lặp đi lặp lại của phép nhân.
- Ví dụ điển hình: Logarit cơ số 10 của 1000 là 3, do bởi 10 mũ 3 là 1000 (1000 = 10 × 10 × 10 = 103); như vậy phép nhân được lặp đi lặp lại ba lần.
- Tổng quát: Lũy thừa cho phép bất kỳ số thực dương nào có thể nâng lên lũy thừa với số mũ thực bất kì, và sẽ luôn luôn tạo ra một kết quả là số dương. Chính vì thế, logarit có thể được tính cho bất kỳ hai số dương thực a và b nào, trong đó a≠1.
Quy tắc tính logarit là gì?
Logarit của một tích
Người ta thường đưa về logarit với cơ số a = 10 (logarit thập phân) để thuận tiện cho tra bảng và tính toán. Còn logarit tự nhiên lấy hằng số e (xấp xỉ bằng 2,718) làm cơ số dùng cho tính toán thông dụng. Logarit nhị phân với cơ số bằng 2 sẽ được sử dụng trong khoa học máy tính.
Logarit của một lũy thừa
Cho hai số dương a, b; với a ≠ 1. Với mọi α ta có: logabα = αlogab
Bảng công thức logarit cơ bản
***Lưu ý: ĐK để logarit có nghĩa là: Cơ số > 0 và #1. Biểu thức dưới dấu logarit phải lớn hơn 0.
Tìm hiểu thêm: Phương pháp tăng giảm khối lượng: Nội dung và Các dạng bài tập
Công thức logarit đổi cơ số
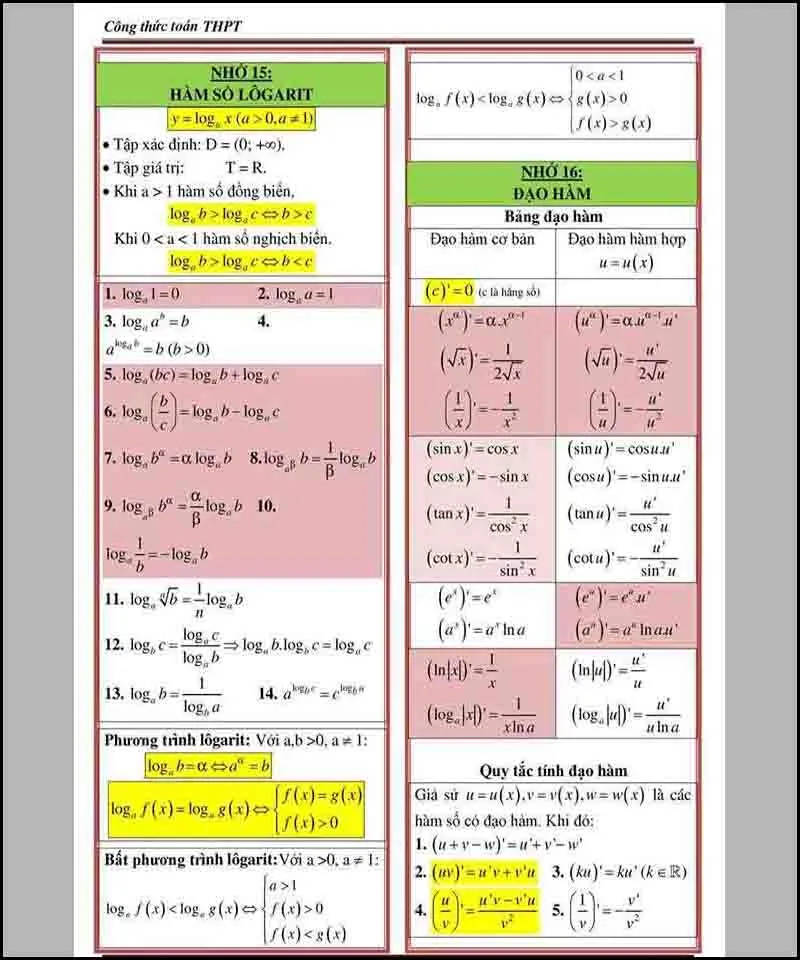
Công thức logarit và đạo hàm
>>>>>Xem thêm: Tỉ khối hơi là gì? Công thức tỉ khối hơi và bài tập áp dụng
Như vậy, bài viết trên đây đã tổng hợp kiến thức về chuyên đề công thức logarit. Hy vọng những kiến thức trong nội dung bài viết sẽ hữu ích với bạn trong quá trình học tập. Chúc bạn luôn học tốt!
